I love updates!
I tried using Pianoteq's new feature - input.
But for some reason, when the limiter is turned on, additional harmonics appear.
This is how it looks like:
Limiter disabled:
Limiter enabled:
This is mistake? It seems like the limiter should not introduce this kind of distortion into the signal.
sound:
https://forum.modartt.com/uploads.php?f...anoteq.mp3
Using Reaper in Ubuntu.
Interesting, but I'm a little confused. Should a limiter add harmonics in its operation? I'll come home in the evening and try another, third-party limiter and compare. Previously, I did not notice distortion, but somehow I chose a game without a limiter. It felt like the sound without the limiter was a little clearer than with. Either something is wrong with the limiter, or the limiter emphasizes some features of the engine, which manifests itself in the appearance of additional harmonics. Or I'm not aware of the features of the limiter.
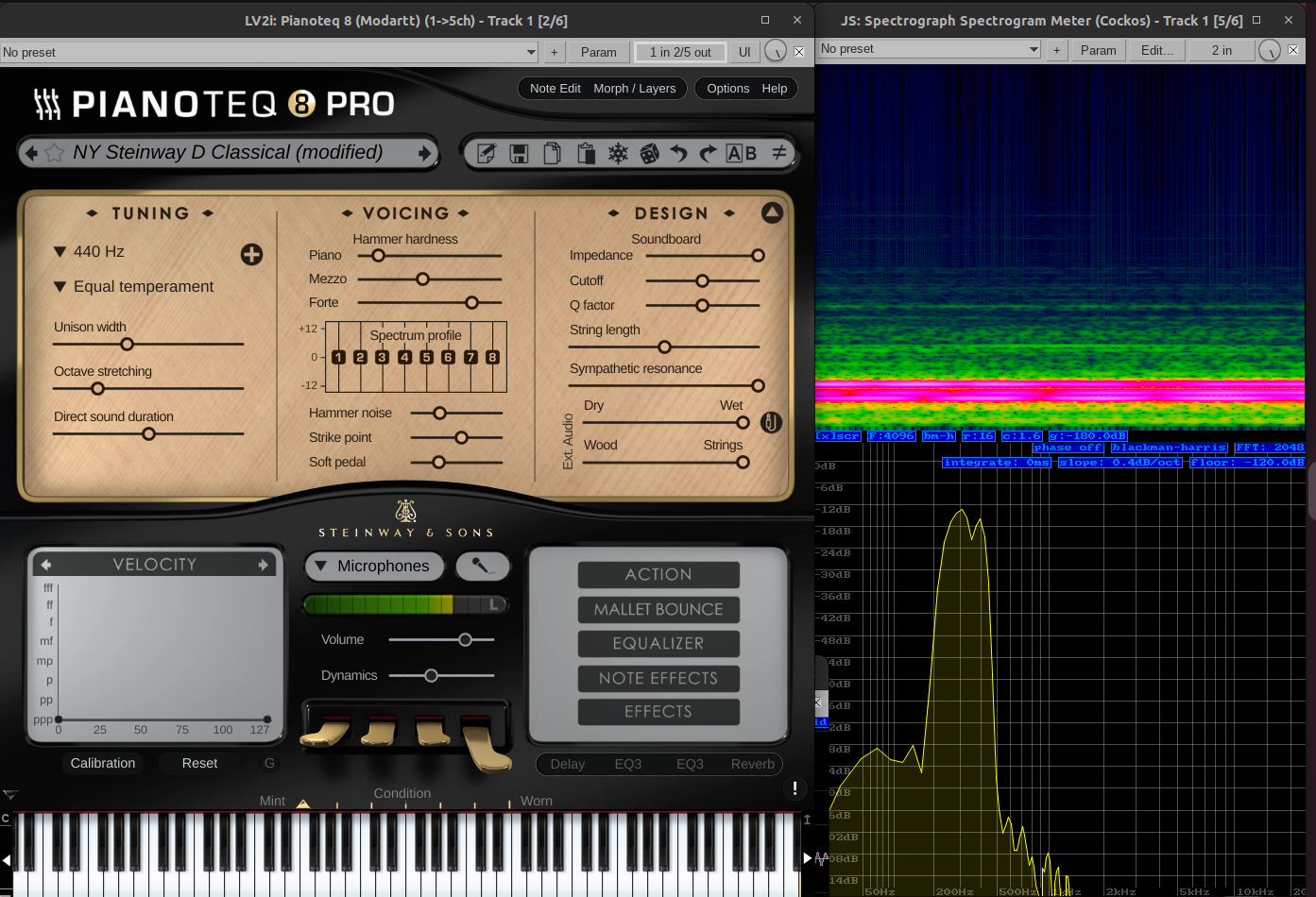
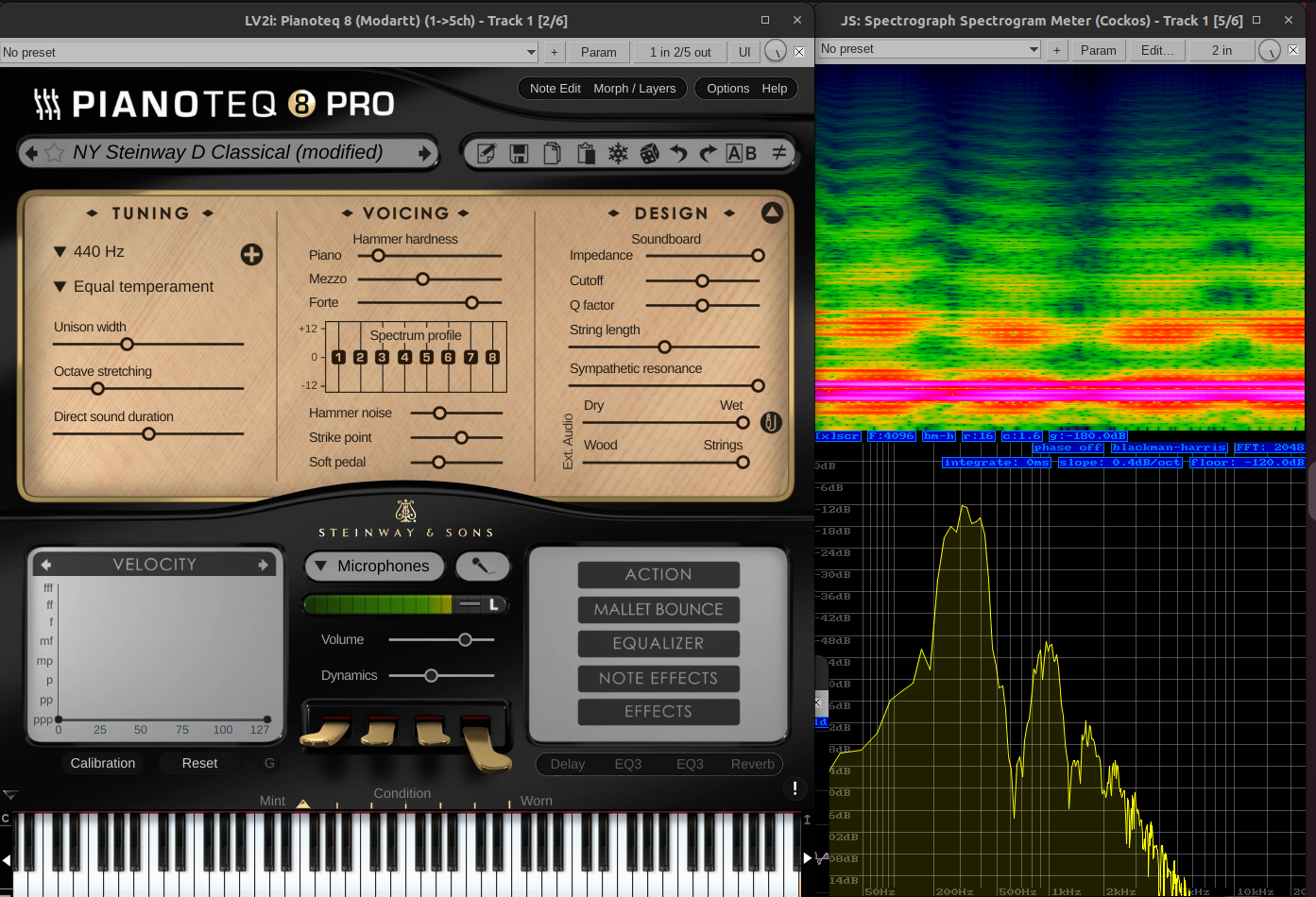
Interesting, but I'm a little confused. Should a limiter add harmonics in its operation?
I am not familiar with the limiter, but let me ask: what would you expect the limiter to do? I would expect it to change the volume to *prevent* additional harmonics to be added when the sound becomes to loud and risk clipping, which would *definitely* add *a lot* of harmonics.
The Fourier transform is linear, so if only volume is changed, no harmonics should be added. However, the change in volume is not constant (otherwise it would be just "lower the volume", not a limiter). The convolution theorem tells that if
* the original sound, function of t, is s(t) and
* another function (limiter causing volume change), is also function of t and called v(t)
* the multiplication of the two (which is probably what the limiter does) s(t) * v(t) has a Fourier transform which is the convolution of the Fourier transforms
So the harmonics definitely change! If the original sound had a very "clean" spectrum, i.e. exactly zero almost anywhere besides some harmonics at specific values, the most that a convolution could do is remove or change the weight of some/all harmonics. But being the original spectrum more complicated, probably not zero almost everywhere, we need to look closely at what the limiter is doing: linear ramps? Piecewise polynomials? Different spectra. Not forgetting that I'm oversimplifying by using the Fourier transform, but that assumes infinite signal, so you probably care about Wavelet transform or another variant of short-time Fourier transform....
Clarification. If I feed the sound through the Pianoteq (curve at "0" and the right pedal pressed), distortion appears when the "Dry" mode is selected. And disappears (or masks) in the "Wet" mode. Also disappears when the limiter is turned off. Somewhere a trick)
Maybe it's a breakdown? :
when change wet/dry and limiter on/off.