Pianoteq Pro sample rate up to 192kHz

Hey,

in simple terms, 192kHz means your density of data is way higher.
Image it, like putting more steps into the same amount of time.

A nice graphic illustrating this:

This means you get more precise information of the actual real frequency at a given time,
because frankly we dont get the real sine wave as pictures, but the value of it OVER TIME, looking more like this:

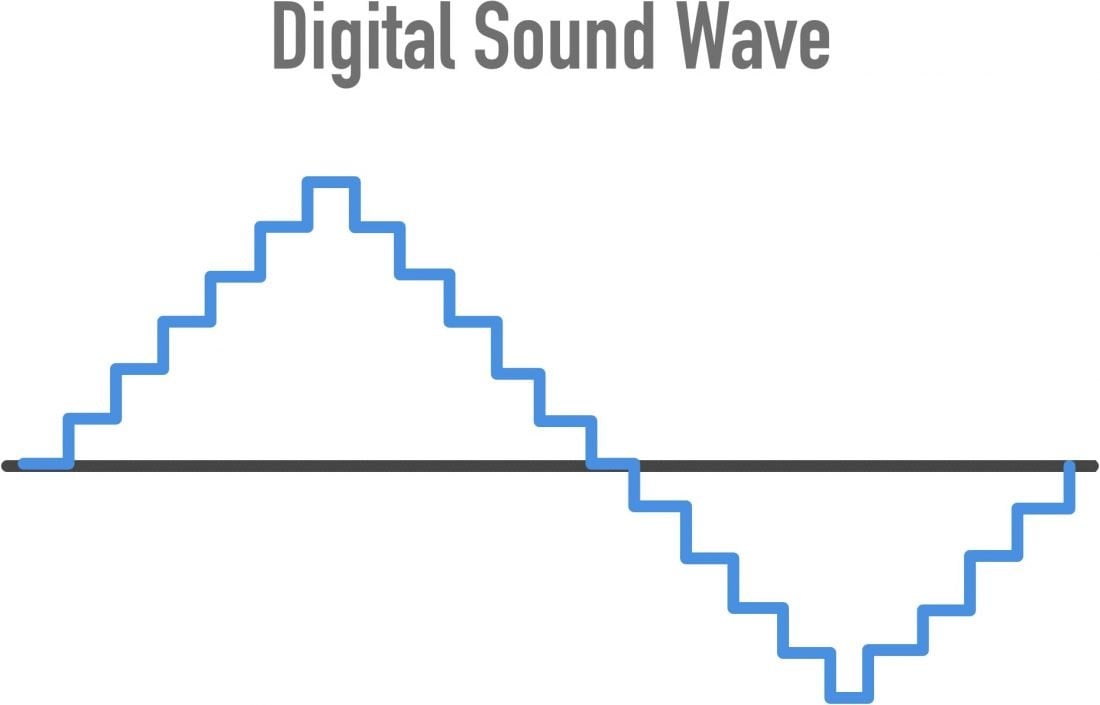
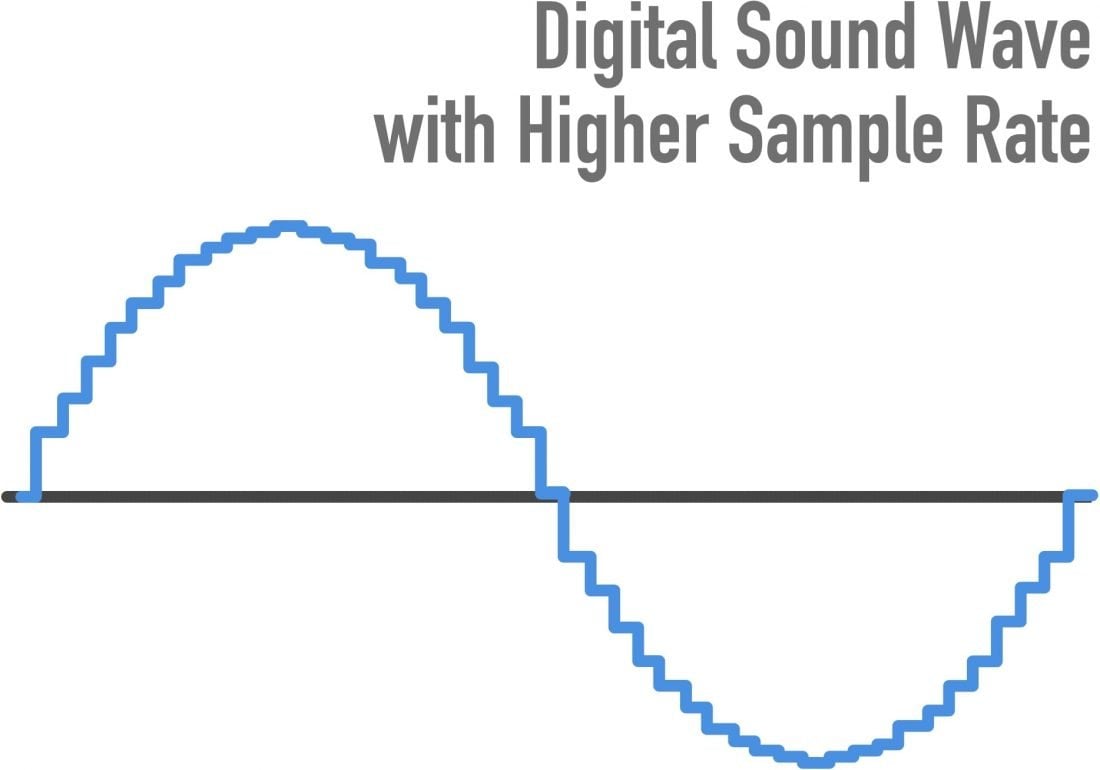
So clearly, more is better.
48 vs 192 kHz obviously needs 4x more computer power.
But as with every mathematical equation, multiplying values gets out of hand quick: So as soon as you try to calculate 4x more data into another set of 4x more data... you see where this is going.

In real world applications, that matters if you want to produce sounds on a professional scale, because you get less artifacts:
You can understand artifacts as mathematical "round up error". Take your 48kHz sample of a piano, and a 48kHz sample of a another sound like a drum. Your result still got 48kHz, so you need to calculate for every Hz how high the interference of this amplitude is. Because the grid is more course, every Hz has a longer timer span it actually covers, your result gets less precise. Your result therefor is off a little bit compared to the real world one would had.

As you can see in the graphs, the typical issue of arc angles in "squaring a circle" is more present the further you get to the "sides" of it - causing less and less precise values with these tones. Imagine it like a spinning wheel that you mark on some point and lay flat: You can see how quick it rotates in the middle when the mark passes by, but it looks close to standing still at the sides while the mark actually travels at the same speed and covers the same distance.

If we do the same with the finer 192kHz grid, your are more close to the actual value that a physical world would have been able to generate by real acoustic waves hitting each other and changing their pattern by interference.
Remember back from physics in school the Avogadro constant? It says smth. like 6.02×10^23 particles in one mol of mass. We could now calculate with the speed of sound in air, and the density of air, how much space this really means and how many particles are in one second of acoustic wave, but to skip all this it roughly means a 23 digit number of "bars" within just once second, where as 192.000 is a 6 digit number.

So you see, real world acoustics got an impressive higher resolution and therefor our course estimation of these can be off.
This is what you hear as artifacts: Sounds that are calculated wrong.

Another thing would be the bit depth, so how many steps are available in each of these "bars" (the amplitude height) above.
These can cause clipping: Again mathematical rounding errors because some theoretical calculated value needed to be cutted off because it would have been between 2 different amplitude heights that your bit depth can represent.

So increasing this depth resolution is again some multiplier, f.e. increasing this by the factor of 2x (depth), together with your previous factor of 4x (sampling rate), and you already require 8x more computer power ... you see again where this is going.

Now imagine both these "height and wide" values are already just course estimations of the real world value, and that you calculate other course values into it. The result getting off more and more... generating sounds that are just wrong.

Can you hear it with Polyphones of just a single Piano: In theory sure.
Does it matter: I boldly claim not so much. 48kHz is good for every usual human, except if you are pretty young and have a really good/trained hearing AND got some real precise playback system. Headphones wont be enough: It requires biiiiig speakers.
When I visit friends in their studios, where they have no sound reflection due do room design, and got 10.000-100.000€ speaker systems, and proper hardware, I can hear artifacts while they master some sounds and it actually is pretty easy to spot them.
But with some regular system at home, suffering already a lot from sound reflections, you will have issues making out the same exact artifacts that you already know.

In my opinion:
If you can afford the Pro version easily, you can for sure just go with it and forget about this issue and know the bottleneck aint the software but your audio setup or your hearing. But its unlikely that you will even notice it without the proper hardware, exp. if you never tasted 192kHz from a really professional setup.

Until 384kHz will be released, and this little voice in our head that always wants the best raises up again telling you to upgrade

But again: All these doubling of resolutions in amplitude height or width is again nothing compared to the power of physics and the Avogadro constant. You will not achieve this kind of precision within the next decades and always be better of buying an acoustic instrument if you want maximum precision than wasting tons of money into digital processing, but you will suffer the issues of real acoustics (instrument design, spatial sound, tuning, space, room design, environmental parameters...) and the costs that come with it.

Make some trade off at some point. Good thing is:
Upgrading PTQ is charging just the exact difference to the next version, so you always spend the same amount.

Greetings from Berlin

https://productionadvice.co.uk/no-stair...tal-audio/

If there’s nothing else the computer in your project will be running, then sure, go crazy with quality settings.

Make sure you get an ultra low latency audio interface like RME so you can actually play at that rate and have low latency without the sound crackling.

One more thing to add though:

Audio quality in the digital domain is a few main things.

Sample rate is one.

Resolution is the other. For example 24 bits means each sample has 2 to the power of 24 possible intensity levels.

Some DAWs process internally at 64 bits to provide huge headroom.

D/A conversion is the third. How the filters and interpolation are done plays a huge role.

24 bits, 96KHz and a good audio interface will provide audio that will satisfy almost any application (there are some unusual applications like audio forensics that benefit from crazy sample rates but for playing back music, 48KHz is more than enough).

And let’s not forget CDs are 16 bit/44KHz, and they sound just fine (D/A conversion is where it’s at for playing back CDs).

I’m stating all this to make clear that you need a pristine chain beginning to end.

Doh, right yesterday I linked this one about folks who are doing what you are doing. Are you one of them?

https://pianoclack.com/forum/d/745-summ...y-projects

Yes, assuming the audio interface is able to keep up.